阅读讲解色彩的美术类书籍的时候，总觉得说得不够明白。什么是纯度、明度，两者不是正交基吗，为什么图上不画出纯度和明度都为最大值的点？为什么存在那么多色彩模型，它们的依据是什么？

作为一个理科生，我需要色彩的数学解释。这种解释可以以一种很精确的方式理解色彩，而且可以为色彩使用做出指导。就像牛顿可以解释小车在力的作用下为什么会如此运动，而且可以预言（在理想情况下）任意时间的任意状态。

我相信色彩是可以计算出来的。和谐的配色一定在数学上存在某种规律¹。只靠感觉会太原始和不精确了，是我不能理解的玄学。当然，这里并没有探讨到艺术的层面，就像相对于和弦音，非和弦音也有它自己的意义。

本文试图在「我想要的理解层次上」给自己一个比较融洽的解释。大致叙述了如何从电磁波的层次建立描述色彩的模型，主要讲述了 CIE ( 国际照明委员会 ) 色彩模型的一些内容。主要参考资料为维基百科和这里²和这里³。这只能算作是笔记或者思考过程，有一些自己不严格（甚至错误的）的理解，一些定义与标准定义也是有偏差的或者错误的。

基础概念

色彩 & 色彩空间

色彩（ Color ）是人的感觉，而不是电磁波的物理特性。由于感觉无法量化，所以我们这样定义色彩: def 色彩是三种视锥细胞感受值的强度的数值组合⁴。

根据三种视锥细胞的刺激程度，便能描述任一种颜色。这种数值组合的值域被称为 LMS 空间。LMS 空间中的每一个点对应了一个颜色。

由于 LMS 空间不便于使用，我们构建了许多色彩模型。def 色彩模型是 LMS 空间到 $\mathbb{R}^3$ 的子空间的映射⁴。这个子空间被称为色彩空间（color space）。然而许多时候，色彩空间被作为色彩模型的同义词来使用。

电磁波与色彩

要区分单一频率光 ( 频率分布在无穷小的区间内 ) 和 广谱光 ( 可能是连续的，也可能是离散的 )。

对于单频光，人眼是足够完备的，可以区分出任意不同频率的电磁波。然而对于广谱光，拥有三种感受器的人眼是不够完备的。有可能存在光谱分布不同，而人眼看到的色彩是一样（对应 LMS 空间中同一个点）的情况。这种现象叫做「异谱同色 ( metamerism ) 」。更多的思考，请看这里。

LMS 空间

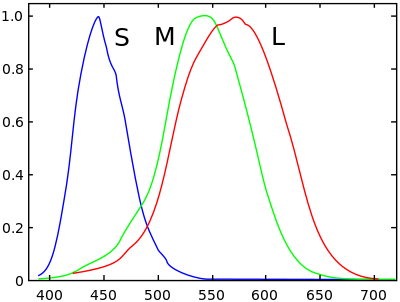
LMS 是 Long、Middle、Short 的缩写，代表对长中短三种波长敏感的感受器（视锥细胞）。从频率分布到 LMS 色彩空间中点的计算如下:

其中 $I$ 为光强，$\overline {s}$ 为上图中的系数。

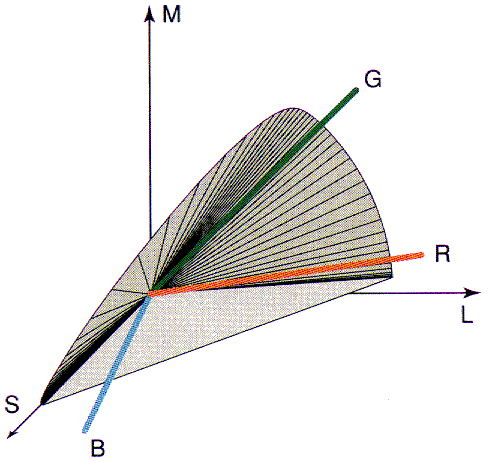
LMS 空间是一个马蹄形的椎体，原点 (0,0,0) 为黑色。LMS 空间并没有覆盖整个 $\mathbb{R}^3$ 的非负空间，我觉得是因为三种视锥细胞的感受范围并不独立。比如 M 基，没有一种频率分布使得只让 M 型感受器接受刺激，而其他两个不被刺激。

CIE 色彩空间

CIE RGB

在能准确测量视锥细胞的响应曲线之前，Wrightand 和 Guild 进行了一个实验以测量从频率到色彩的映射关系。

由于 LMS 空间不能直接测量，这里选取「人类的感觉」作为色彩的代表。

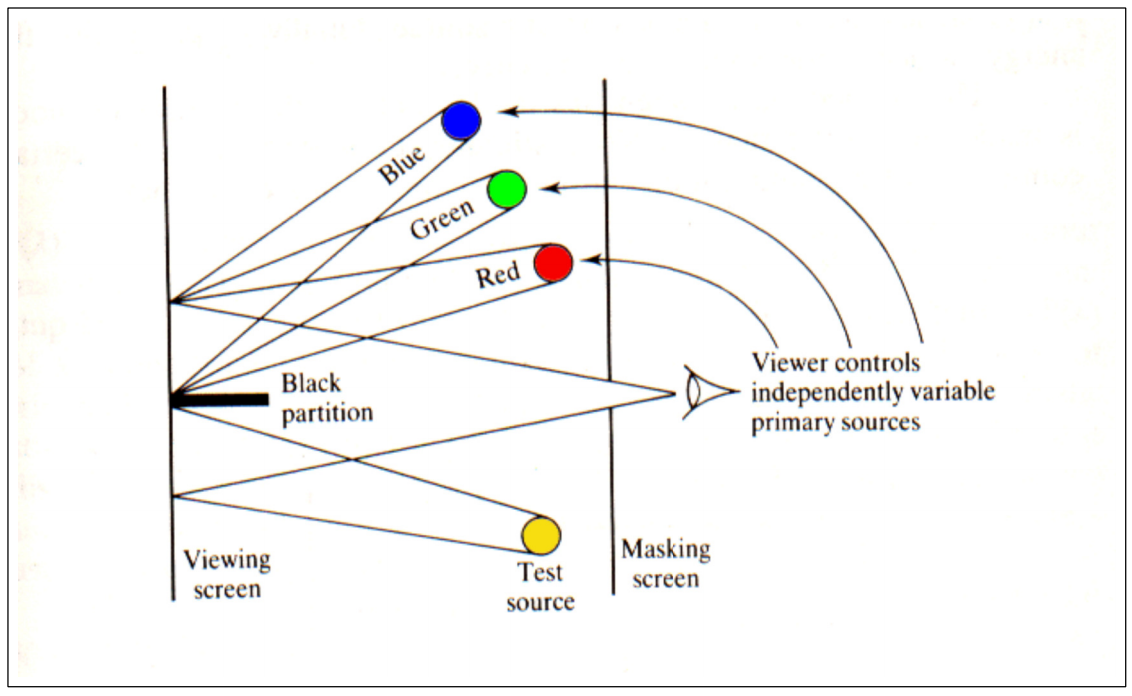
我们知道 LMS 空间中的三个基大致对应于 R G B 三种色彩 ( 其实就是红绿蓝，只不过它究竟是什么颜色我们来没有意义 ) ，所以我们选取这三种颜色的对各种颜色进行合成。通过调节 R G B 三种光源的比例，使得两遍的颜色看起来是一样的。

这个实验得到了单色光和三基色光源的对应关系，即得到了一个色彩空间⁵，称为 CIE RGB 色彩空间。

实验的一些细节:

• 选取的 RGB 三种色彩分别为 700 nm (red), 546.1 nm (green) and 435.8 nm (blue) 波长的单色光。 选取后两者主要是因为易于重现 ( reproduce )，而 700 nm 是因为，在难以重现的频段，眼睛对此频率的误差不敏感。( 个人感觉这些波长的选取是很随意的，但由于后一条的原因，这种选取是不影响准确性的。)
• R G B 三种单色光并不能重现所有颜色（后面解释）。 为了可以使颜色可以合成，我们在目标上加小量单色光 ( RGB 中的一种 )，这个量被算作复数计入映射函数中，所以映射函数中有负值的存在。

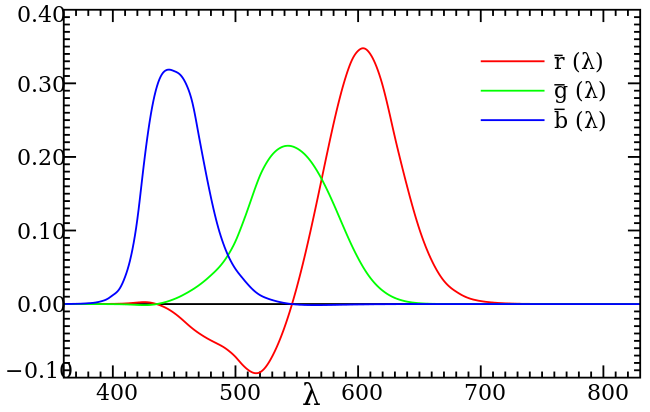
此为映射函数 ( color-matching function )。注意 CIE RGB 空间中的值有可能为负的。全为非负数的子空间是无法完全描述所有色彩的。

一个广谱光的 R G B 值，可以由 $\overline {r}(\lambda)$ $\overline {g}(\lambda)$ $\overline {b}(\lambda)$ 函数积分而来。 $\overline {r}(\lambda)$ $\overline {g}(\lambda)$ $\overline {b}(\lambda)$ 是归一化过的，所以对于平直波谱，其 RGB 为 (1, 1, 1)。

CIE XYZ 色彩空间的构建

Grassmann’s law:

人眼对色彩的感知（大约）是线性的: 如果有光束 1 对应 RGB 空间的点 p1，和光束 2 对应的 p2，那么两个光束混合后对应的点为 p1 + p2。

Luminosity function:

人眼对于不同波长的电磁波的感知亮度是不一样的。Luminosity function 是客观的辐射能量 与 人眼主观可感受的辐射能量 的比例系数。

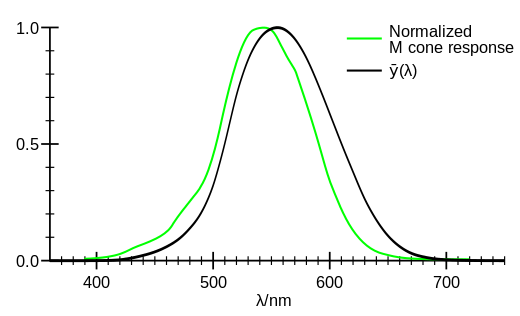
它大致在 550nm 处达到峰值，与 M 感受器的曲线相似。( 也就是同等辐射强度的光，越偏绿感受到的 luminance 越大。) 用 $V(\lambda)$ 表示。

虽然 $V(\lambda)$ 与波长有关，但是在波长一定的情况下，可以通过增加光通量来增大 luminance。⁶

构建:

在假定 Grassmann’s law 成立的前提下，一个色彩空间可以由 CIE RGB 空间施加一个线性变换得到。

CIE XYZ 是一种 CIE RGB 的线性变化，X Y Z 满足如下条件:

• X Y Z 为非负值
• The $y(\lambda)$ color matching function would be exactly equal to the photopic luminous efficiency function $V(\lambda)$
• 白色在 $ (x, y, z) = (1/3, 1/3, 1/3)$ 处
• ……

具体实现为:

Color-Matching function 为

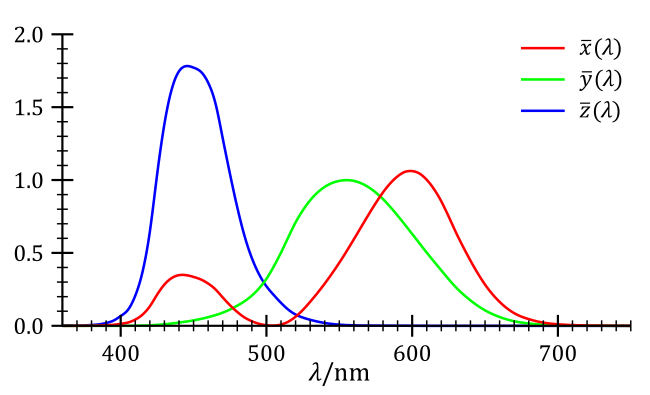
由于 $y(\lambda)$ 与 M 感受曲线是相似的，Z 又人为地选取与 S 相似的曲线，所以 XYZ 空间的基于 LMS 空间的基是相似的。一个色彩在 XYZ 空间中的坐标与咋 LMS 空间中的坐标是相似的（但是不同）。

CIE xyY 色度图

对于一种单色光，增加它的辐射强度，它对应的 LMS 值会等比增加。我们认为 LMS 值的比例为该「频率分布」的色度。与 LMS 空间类似，CIE RGB 空间中，单色光辐射强度增加，RGB 会成比例增加（根据 Grassmann’s law，两束同样的单色光叠加，RGB 的值会成比例增加），那么 RGB 的比例也是色度的一种定义。我们姑且认为这两种定义是等价的⁷（等同于 RGB 空间是 LMS 的线性变换）。

由于 CIE XYZ 空间是 CIE RGB 空间的线性变换，那么 X Y Z 可以写成

那么系数 $k$ 蕴含了亮度的信息（我们还没有定义亮度 ）。

如果只看 x y z ，那么我们就忽略了色彩中的「亮度」相关的信息，而只关注色度。由于 $x+y+z = 1$ ，z 可以由 x y 导出，所以 x y 的值域就可以表示所有色度。

x y 只能表示色度，丢失了「亮度」的信息。尽管我可以选取系数 $k$ 代表亮度信息，但是为了方便我们采用 Y 作为亮度信息的补充。这样一组 x y Y 值能代表一个色彩，x y Y 的值域称为 xyY 色彩空间。

x y 的值域是 CIE XYZ 空间在 $X+ Y + Z = 1$ 的截面对于 X Y 平面的投影。该投影称为 CIE xy 色度图。

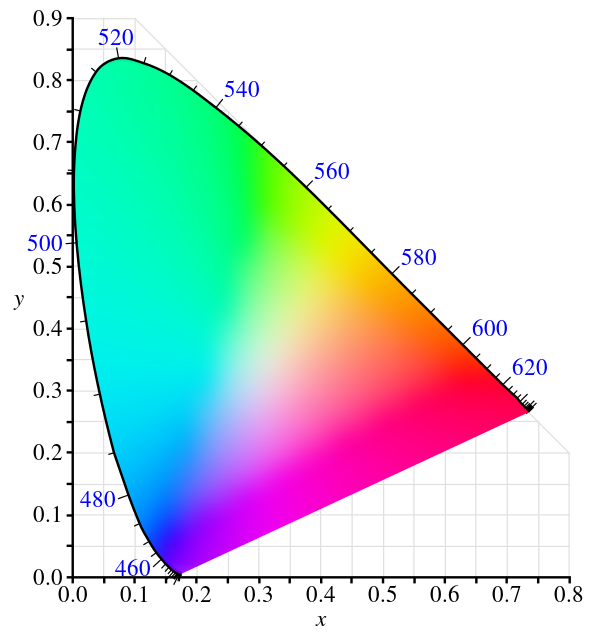
它的一些特性:

• 它展示了人类可见的所有色度
• 色域的曲线边界叫做“光谱轨迹”，是单色光对应的颜色，曲线旁的数字代表相应单色光的波长
• 平直频谱光 ( 白色点 ) 对应 (1/3, 1/3) 处 ( 这是 XYZ 空间定义的 )
• 两点之间直线上任何颜色都可以用这两个颜色混合出来
• 两个同等明亮颜色的等量混合一般不位于这个线段的中点，即图上距离不对应于两种颜色之间的差别程度。比如在绿色附近，一定距离的两点的颜色差别比蓝色附近相同距离的颜色差别更小。

可以看到，图中红绿蓝三点构成的三角形并不能覆盖所有色域。这就解释了 CIE RGB 非负子空间不能显示所有颜色。覆盖整个色域的三角形的顶点是不存在的（最根本是由于三种视锥感受范围的重合）。

色调 饱和度 明度

在给出色调、饱和度的准确定义前，我们可以直观地描述一下这两个量的特性。

在 xy 色度图中，白色点饱和度设为 0，光谱轨迹的点的饱和度为 100%。

白色点与谱色轨迹上任一点相连的直线上的点，都具有相同的色调。由于两点可以合成之间连线上的色彩，这些色彩可以认为是单色光与白光的不同比例的混合。（单色光与白光的关系好像音调与泛音呀。）

更多导出的色彩空间

由于 CIE xyY 空间 等距两点的颜色差别程度不同，所以提出了许多色彩模型来弥补这个不足。下面的几个模型都是 XYZ色彩空间的非线性变化。

CIE 1960 YUV

保留 Y ，U V 为 x y 的非线性变换⁸，使得在色度图中，对颜色感知的差别是均匀的。

CIE LUV

为了解决 Y 的非线性问题，引入 L* (lightness，只是 Y 的函数)，同时也解决了 X Y 的非线性性。LUV 空间中的欧式距离可以度量 color difference。

LCH_uv : 为 LUV 的极坐标版，也叫 CIE LCh_uv (C for chroma, h for hue) 。具体内容见这里。

CIE 1976 LAB

Lab color is designed to approximate human vision. It aspires to perceptual uniformity, and its L component closely matches human perception of lightness.⁹

Lab values do not define absolute colors unless the white point is also specified.

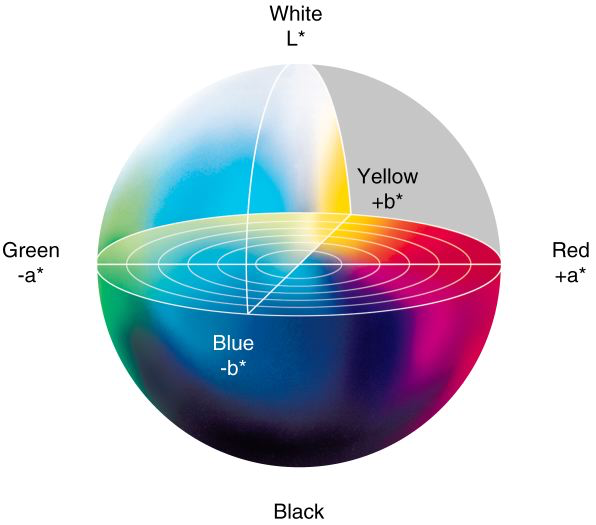
LAB 极坐标版称为 LCh_ab。LAB 与 XYZ 空间的具体变换见这里。

再看色调 饱和度 明度

通过这几个系统，色调 亮度 饱和度应该很容易定义了。比如在 LAB 中，L 可以理解为亮度，a b 的极坐标表示可以理解为 色调 hue 和 饱和度（其实在 LAB 系统中应该叫 Chroma）。

由于 L 只是 Y 的函数，之前定义的「色度」与这里的色调+饱和度是等价的。

设备有关色彩空间

CIE 色彩模型是一个绝对的色彩模型，从频谱分布直接到色彩数值。而平时常见 RGB YUV 和 CMYK 色彩模型并是与设备有关的。比如 RGB，R G B 三个基对应的绝对数值是在不同设备上是有所差异的，单纯的 RGB 坐标是没有意义的。（ sRGB 的基是固定的，也是一种绝对色彩模型。）

结束语

在色彩模型的建立中，有许多近似与非线性（比如 Grassmann’s law），这可能是源于生物体的不精确性。写到这里，开篇对于色彩数值规律的先验性的憧憬也许被打破了。但如果一个好的色彩模型可以将这些「妥协」封装在模型内部，暴露出来的是纯粹的理念上的「色彩」，那么我仍觉得好看的色彩会有数学上的协调性。

学习这部分内容的时候，找到的（通俗易懂的系统的）资料很少，应该有很多东西理解得不够准确。搜到这本书 Color Theory and Its Application in Art and Design，是覆盖本文内容的一份严谨的论述。只可惜没有找到阅读的途径（卖得太贵了）。

除了从理念上理解色彩的建模外，这里做一个小小的尝试。左边的粉色是已有色彩，转换成 LAB 坐标后，a b 值取反，得到它的（精确的）补色，耗时接近于 0。